Breadth-First Search Algorithm
Graph traversal methods are used in various applications in the real-world environment from performing peer-to-peer communication to finding the nearest cafes using GPS.
The Breadth-First Search Algorithm is being discussed here in this Blog along with graph traversal methods using examples for an in-depth understanding of learners and aspirants around the world.
We cover an introduction to graph traversal, Breadth-First Search Algorithm, pseudocode of Breadth-First Search Algorithm, and its applications.
What is Graph Traversal?
A graph traversal is a task of visiting and exploring a graph for processing. It is about visiting and exploring every vertex and edge in a graph for that all the vertices are explored at once exactly. Breadth-first search is one of the familiar algorithms in a graph traversal technique. It is widely used for solving complex problems.
What is Breadth-First Search Algorithm?
As mentioned earlier, the Breadth-First Search Algorithm is one of the graph traversal techniques where we select a random node as an initial node and begin to traverse the graph in a layer-wise way for visiting and exploring all the nodes and child nodes at least once.
Here is an example that explains breadth-first search with visiting and exploring nodes.
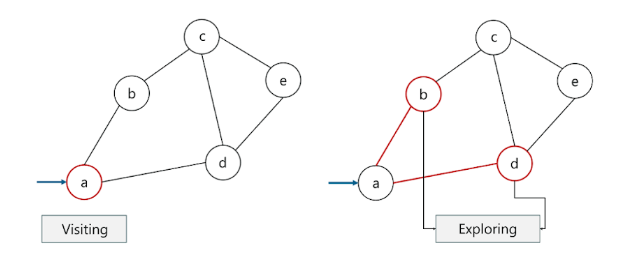
Here, visiting a node is to visit or select a node, and exploring a node is to explore the adjacent nodes (child nodes) of a selected node.
Example for Breadth-First Search Algorithm
Breadth-First Search is a level-based and simple Algorithm for solving a problem. Our goal is to traverse the graph (given binary tree) by using the Breadth-First Search Algorithm
It is important to have an in-depth understanding of the primary data structure that is involved in the Breadth-First Search Algorithm. Consider a queue that follows a structure of the first-in-first-out method. It will be open on both ends for inserting data on one side (en queue) and removing data on the other side (de queue).
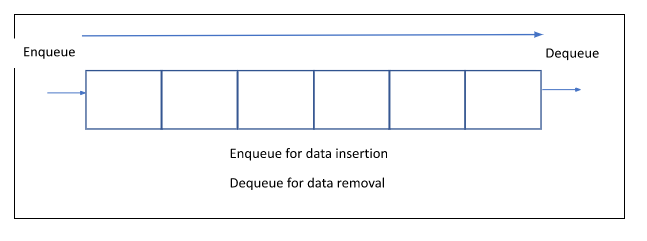
Following are the steps that are involved in traversing a graph using Breadth-First Search Algorithm
Step 1: Get an Empty Queue
Step 2: Choose a starting node and insert it into the Queue
Step 3: Extract the node from the Queue to insert its child nodes (exploring a node) into the Queue
Step 4: Display the extracted node
Example
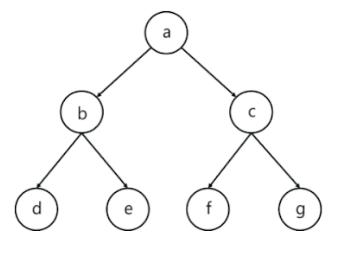
Here, we have assigned node ‘a’ as the root and begin our traversing downward to follow the above steps repeatedly to add explore child nodes.
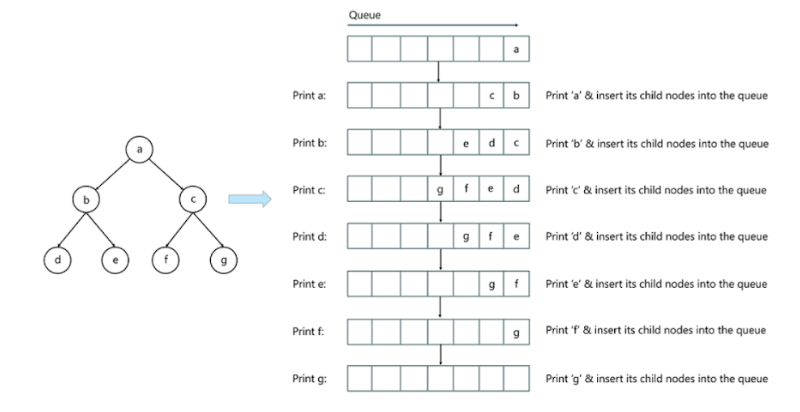
This image describes the end-to-end process of the Breadth-First Search Algorithm and it is as follows
- Assigning ‘a’ node as the parent or root node and inserting it into the queue
- Extract the ‘a node from the queue to insert its child nodes of ‘b’ and ‘c’.
- Print node ‘a’
- Now, the queue is not empty as it has ‘b’ and ‘c’ nodes. As ‘b’ is the first node in the queue, we can extract it to the queue and insert its child nodes of ‘b’ such as ‘d’ and ‘e’.
- Repeat the steps until the queue will be empty. Here, we shouldn’t add the nodes that are already added into the queue.
Pseudocode of Breadth-First Algorithm
Following is the code that defines a breadth-first algorithm
Input: s as the source node
BFS (G, s)
let Q be queue.
Q.enqueue( s )
mark s as visited
while ( Q is not empty)
v = Q.dequeue( )
for all neighbors w of v in Graph G
if w is not visited
Q.enqueue( w )
mark w as visited
The following steps have been achieved through the above codes.
Step 1: (G, s ) is given as input. G denotes graph and s denotes the root node
Step 2: ‘Q’ defines a queue that has been created and initialized with the source node ‘s’.
Step 3: Every child node of ‘s’ has been marked
Step 4: Extract ‘s’ from the queue and visit its child nodes respectively.
Step 5: Begin to proceed with all the child nodes of ‘v’.
Step 6: Save the child node that is defined by w in Q and make further visits to its other child nodes.
Step 7: Repeat the process until the Q is empty.
Real-life applications of Breadth-First Search Algorithm
Breadth-First Search Algorithm is used in a variety of real-time applications and the following are some of the important use cases.
Search Engine Crawlers: Breadth-First Search Algorithm is the main algorithm for crawlers of search engines used to index the web pages. It will be started from the source page and follows the link related to the root page. Here, every page is considered a node in a graph.
GPS Navigation Systems: To find neighboring locations on GPS using a Breadth-First Search Algorithm
Find the shortest path for minimizing the spanning tree for an unweighted graph: Calculating the shortest path is simple for unweighted graphs as it chooses a path with the least number of edges. Breadth-first search allows traversing a graph with a minimum number of nodes that are starting from the source or parent node.
Broadcasting: Networks are working based on the packets for communication and the packets are following a traversal method for reaching various networking nodes. It is using Breadth-First Search Algorithm for communicating broadcasted packets over all the nodes of the network.
Peer to Peer Networking: It is using a popular traversal method, breadth-first search to find all the neighboring nodes. BitTorrent is the best example that uses a Breadth-First Search Algorithm for peer-to-peer communication.
Conclusion
The Breadth-First Search Algorithm is used widely in various data and networking-related fields. The understanding of the Breadth-First Search Algorithm helps you to implement it according to the exact needs of machine learning processes. Learn Machine Learning Course in Chennai at Softlogic Systems to gain expertise with hands-on exposure to the Breadth-First Search Algorithm.

